python drive.py -l lombard -i none

Modeling car locations

At each time step $t$, let $C_t \in \mathbb R^2$ be a pair of coordinates representing the actual location of the single other car (which is unobserved). We assume there is a local conditional distribution $p(c_t \mid c_{t-1})$ which governs the car's movement. Let $a_t \in \mathbb R^2$ be your car's position, which you observe and also control. To minimize costs, we use a simple sensing system based on a microphone. The microphone provides us with $D_t$, which is a Gaussian random variable with mean equal to the true distance between your car and the other car and variance $\sigma^2$ (in the code, $\sigma$ is Const.SONAR_STD, which is about two-thirds the length of a car). In symbols,

For example, if your car is at $a_t = (1,3)$ and the other car is at $C_t = (4,7)$, then the actual distance is $5$ and $D_t$ might be $4.6$ or $5.2$, etc. Use util.pdf(mean, std, value) to compute the probability density function (PDF) of a Gaussian with given mean mean and standard deviation std, evaluated at value. Note that evaluating a PDF at a certain value does not return a probability -- densities can exceed $1$ -- but for the purposes of this assignment, you can get away with treating it like a probability. The Gaussian probability density function for the noisy distance observation $D_t$, which is centered around your distance to the car $\mu = \|a_t - C_t\|$, is shown in the following figure:

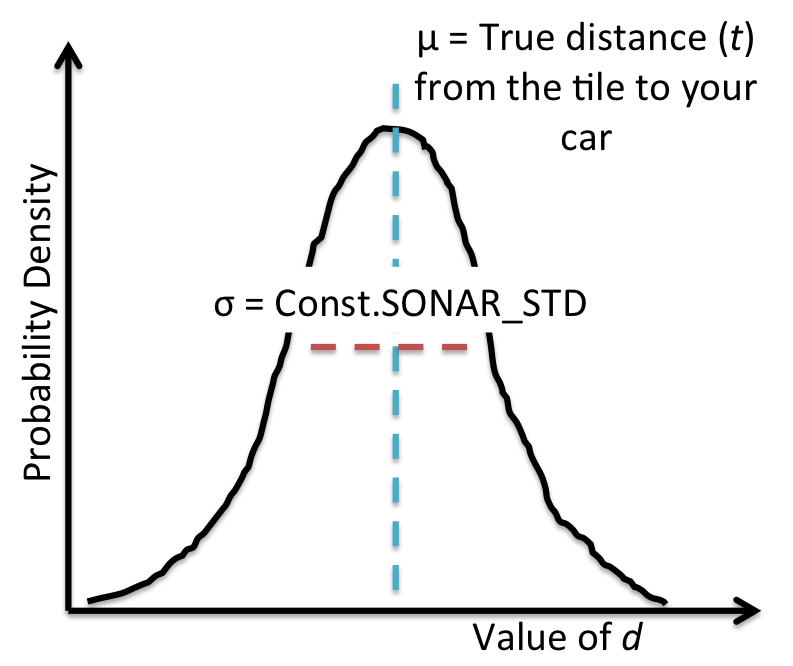
Your job is to implement a car tracker that (approximately) computes the posterior distribution $\mathbb P(C_t \mid D_1 = d_1, \dots, D_t = d_t)$ (your beliefs of where the other car is) and update it for each $t = 1, 2, \dots$. We will take care of using this information to actually drive the car (i.e., set $a_t$ to avoid a collision with $c_t$), so you don't have to worry about that part.

To simplify things, we will discretize the world into tiles represented by (row, col) pairs, where 0 <= row < numRows and 0 <= col < numCols. For each tile, we store a probability representing our belief that there's a car on that tile. The values can be accessed by: self.belief.getProb(row, col). To convert from a tile to a location, use util.rowToY(row) and util.colToX(col).

Here's an overview of the assignment components:

• In Problems 1 and 2 (code), you will implement ExactInference, which computes a full probability distribution of another car's location over tiles (row, col).
• In Problem 3 (code), you will implement ParticleFilter, which works with particle-based representation of this same distribution.
• Problem 4 (written) gives you a chance to extend your probability analyses to a slightly more realistic scenario where there are multiple other cars and we can't automatically distinguish between them.

A few important notes before we get started:

• Past experience suggests that this will be one of the most conceptually challenging assignments of the quarter for many students. Please start early, especially if you're low on late days!
• We strongly recommend that you attend/watch the lectures on Bayesian networks and HMMs before getting started, and keep the slides handy for reference while you're working.
• The code portions of this assignment are short and straightforward -- no more than about 30 lines in total -- but only if your understanding of the probability concepts is clear! (If not, see the previous point.)
• As a notational reminder: we use the lowercase expressions $p(x)$ or $p(x|y)$ for local conditional probability distributions, which are defined by the Bayesian network. We use the uppercase expressions $\mathbb P(X = x)$ or $\mathbb P(X = x | Y = y)$ for joint and posterior probability distributions, which are not pre-defined in the Bayesian network but can be computed by probabilistic inference. Please review the lecture slides for more details.

In this problem, we assume that the other car is stationary (e.g., $C_t = C_{t-1}$ for all time steps $t$). You will implement a function observe that upon observing a new distance measurement $D_t = d_t$ updates the current posterior probability from $$\mathbb P(C_t \mid D_1 = d_1, \dots, D_{t-1} = d_{t-1})$$ to $$\mathbb P(C_t \mid D_1 = d_1, \dots, D_t = d_t) \propto \mathbb P(C_t \mid D_1 = d_1, \dots, D_{t-1} = d_{t-1}) p(d_t \mid c_t),$$ where we have multiplied in the emission probabilities $p(d_t \mid c_t)$ described earlier under "Modeling car locations". The current posterior probability is stored as self.belief in ExactInference.

1. Fill in the observe method in the ExactInference class of submission.py. This method should modify self.belief in place to update the posterior probability of each tile given the observed noisy distance to the other car. After you're done, you should be able to find the stationary car by driving around it (using the flag -p means cars don't move):

Notes:

• Once you implement the observe function, you can start driving with exact inference.

  python drive.py -a -p -d -k 1 -i exactInference

  You can also turn off -a to drive manually.
• Read through the code in util.py for the Belief class before you get started... you'll need to use this class for several of the code tasks in this assignment.
• Remember to normalize the posterior probability after you update it. (There's a useful function for this in util.py).
• On the small map, the autonomous driver will sometimes drive in circles around the middle block before heading for the target area. In general, don't worry too much about the precise path the car takes. Instead, focus on whether your car tracker correctly infers the location of other cars.
• Don't worry if your car crashes once in a while! Accidents do happen, whether you are human or AI. However, even if there was an accident, your driver should have been aware that there was a high probability that another car was in the area.

Now, let's consider the case where the other car is moving according to transition probabilities $p(c_{t+1} \mid c_t)$. We have provided the transition probabilities for you in self.transProb. Specifically, self.transProb[(oldTile, newTile)] is the probability of the other car being in newTile at time step $t+1$ given that it was in oldTile at time step $t$.

In this part, you will implement a function elapseTime that updates the posterior probability about the location of the car at a current time $t$ $$\mathbb P(C_t = c_t \mid D_1 = d_1, \dots, D_t = d_t)$$ to the next time step $t+1$ conditioned on the same evidence, via the recurrence: $$\mathbb P(C_{t+1} = c_{t+1} \mid D_1 = d_1, \dots, D_t = d_t) \propto \sum_{c_t} \mathbb P(C_t = c_t \mid D_1 = d_1, \dots, D_t = d_t) p(c_{t+1} \mid c_t).$$ Again, the posterior probability is stored as self.belief in ExactInference.

1. Finish ExactInference by implementing the elapseTime method. When you are all done, you should be able to track a moving car well enough to drive autonomously by running the following.

python drive.py -a -d -k 1 -i exactInference

Notes:

• You can also drive autonomously in the presence of more than one car:

  python drive.py -a -d -k 3 -i exactInference

• You can also drive down Lombard:

  python drive.py -a -d -k 3 -i exactInference -l lombard

  On Lombard, the autonomous driver may attempt to drive up and down the street before heading towards the target area. Again, focus on the car tracking component, instead of the actual driving.

Though exact inference works well for the small maps, it wastes a lot of effort computing probabilities for every available tile, even for tiles that are unlikely to have a car on them. We can solve this problem using a particle filter. Updates to the particle filter have complexity that's linear in the number of particles, rather than linear in the number of tiles.

For a great conceptual explanation of how particle filtering works, check out this video on using particle filtering to estimate an airplane's altitude.

In this problem, you'll implement two short but important methods for the ParticleFilter class in submission.py. When you're finished, your code should be able to track cars nearly as effectively as it does with exact inference.

1. Some of the code has been provided for you. For example, the particles have already been initialized randomly. You need to fill in the observe and elapseTime functions. These should modify self.particles, which is a map from tiles (row, col) to the number of particles existing at that tile, and self.belief, which needs to be updated each time you re-sample the particle locations.

You should use the same transition probabilities as in exact inference. The belief distribution generated by a particle filter is expected to look noisier compared to the one obtained by exact inference.

python drive.py -a -i particleFilter -l lombard

Note: The random number generator inside util.weightedRandomChoice behaves differently on different systems' versions of Python (e.g., Unix and Windows versions of Python). We STRONGLY recommend running the code locally on a Python 3.7+ installation for consistency with the autograder.

So far, we have assumed that we have a distinct noisy distance reading for each car, but in reality, our microphone would just pick up an undistinguished set of these signals, and we wouldn't know which distance reading corresponds to which car. First, let's extend the notation from before: let $C_{ti} \in \mathbb R^2$ be the location of the $i$-th car at the time step $t$, for $i = 1, \dots, K$ and $t = 1, \dots, T$. Recall that all the cars move independently according to the transition dynamics as before.

Let $D_{ti} \in \mathbb R$ be the noisy distance measurement of the $i$-th car at time step $t$, which is now not directly observed. Instead, we observe the unordered set of distances $D_t = \{ D_{t1}, \dots, D_{tK} \}$ as a collective and so cannot attribute any individual measurement in this set to a specific car. (For simplicity, we'll assume that all distances are distinct values.) In other words, you can think of this scenario as the same as observing the list $E_t = (E_{t1}, \dots, E_{tK})$ which is a uniformly random permutation of the (noisy) correctly ordered distances $(D_{t1}, \dots, D_{tK})$ where index $i$ represents the noisy distance to car $i$ at time $t$.

For example, suppose $K=2$ and $T = 2$. Before, we might have gotten distance readings of $1$ and $2$ for the first car and $3$ and $4$ for the second car at time steps $1$ and $2$, respectively. Now, our sensor readings would be permutations of $\{1, 3\}$ (at time step $1$) and $\{2, 4\}$ (at time step $2$). Thus, even if we knew the second car was distance $3$ away at time $t = 1$, we wouldn't know if it moved further away (to distance $4$) or closer (to distance $2$) at time $t = 2$.

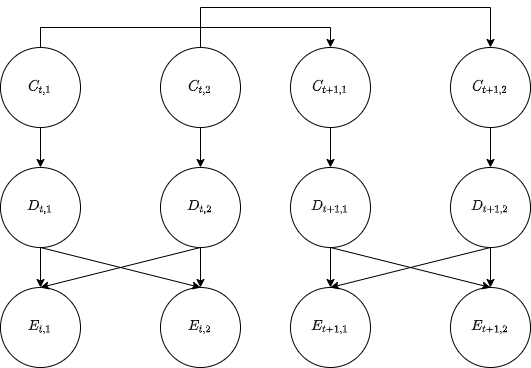
Here is a diagram of the Bayes net corresponding to the above situation, for the case where $K = 2$ and only showing two timesteps, $t$ and $t+1$. Note that because the observed distances $E_{ti}$ are a permutation of the true distances $D_{ti}$, each $E_{ti}$ depends on all of the $D_{ti}$.

1. Suppose we have $K=2$ cars and one time step $T=1$. Write an expression for the conditional distribution $\mathbb P(C_{11} = c_{11}, C_{12} = c_{12} \mid E_1 = e_1)$ as a function of the PDF of a Gaussian $\mathcal p_{\mathcal N}(v; \mu, \sigma^2)$ and the prior probability $p(c_{11})$ and $p(c_{12})$ over car locations. Your final answer should not contain variables $d_{11}$, $d_{12}$.

   Remember that $\mathcal p_{\mathcal N}(v; \mu, \sigma^2)$ is the probability of a random variable, $v$, in a Gaussian distribution with mean $\mu$ and standard deviation $\sigma$.

   Hint: for $K=1$, the answer would be $$\mathbb P(C_{11} = c_{11} \mid E_1 = e_1) \propto p(c_{11}) p_{\mathcal N}(e_{11}; \|a_1 - c_{11}\|, \sigma^2).$$ where $a_t$ is the position of the car at time t. To better inform your use of Bayes' rule, you may find it useful to draw the Bayesian network and think about the distribution of $E_t$ given $D_{t1}, \dots, D_{tK}$.

   Hint: Note that the observed variable(s) are the shuffled/randomized distances $\mathbb E_t = [E_{t1}, E_{t2}, ..., E_{tK}]$. These are a random permutation of the unobserved true distances $\mathbb D_t = [D_{t1}, D_{t2}, ..., D_{tK}]$, where $D_{t1}$ is the distance of car $1$ at timestep $t$. Note that $E_{t1}$ is the emission from one of the cars at timestep $t$, but we aren't sure which one (it is NOT necessarily car 1, it could be any of the cars). On the other hand, $D_{t1}$ is the measured distance of car 1 (we know with certainty that it comes from car 1), the only issue is that we don't observe it directly.

   Hint: To reduce notation, you may write, for example, $p(c_{11}∣e_{11})$ instead of $\mathbb P(C_{11}=c_{11}∣E_{11}=e_{11})$.

   A mathematical expression relating $P(C_{11} = c_{11}, C_{12} = c_{12} | E_1 = e_1)$ with the PDF of a Gaussian and the priors $P(c_{11})$ and $P(c_{12})$ over car locations
2. Assuming the prior $p(c_{1i})$ of where the cars start out is the same for all $i$ (i.e. for all K cars), show that the number of assignments for all $K$ cars $(c_{11}, \dots, c_{1K})$ that obtain the maximum value of $\mathbb P(C_{11} = c_{11}, \dots, C_{1K} = c_{1K} \mid E_1 = e_1)$ is at least $K!$.

   You can also assume that the car locations that maximize the probability above are unique ($C_{1i} \neq c_{1j}$ for all $i \neq j$).

   Hint: The priors $p(c_{1i})$ are a probability distribution over the possible starting positions ($t=1$) of each car $i$. Note that even if the car positions share the same prior, it doesn't necessarily mean they have the exact same start positions $c_{1i}$ because the start positions are sampled from the prior distribution, which can yield different values each time it is sampled from. However, you should think about what the priors all being the same means intuitively in terms of how we can associate observations with cars.

   Note: you don't need to produce a complicated proof for this question. It is acceptable to provide a clear explanation based on your intuitive understanding of the scenario.

   Either a short mathematical argument or concise explanation for why the statement defined in the problem is true.
3. (extra credit) For general $K$, what is the treewidth corresponding to the posterior distribution over all $K$ car locations at all $T$ time steps conditioned on all the sensor readings: $$\mathbb P(C_{11} = c_{11}, \dots, C_{1K} = c_{1K}, \dots, C_{T1} = c_{T1}, \dots, C_{TK} = c_{TK} \mid E_1 = e_1, \dots, E_T = e_T)?$$ Briefly justify your answer.
   The treewidth as a function of $K$ and a justification for why the treewidth is represented by that function.
4. (extra credit) Now suppose you change your sensors so that at each time step $t$, they return the list of exact positions of the $K$ cars, but shifted (with wrap around) by a random amount. For example, if the true car positions at time step $1$ are $c_{11} = 1, c_{12} = 3, c_{13} = 8, c_{14} = 5$, then $e_1$ would be $[1, 3, 8, 5]$, $[3, 8, 5, 1]$, $[8, 5, 1, 3]$, or $[5, 1, 3, 8]$, each with probability $1/4$. Describe an efficient algorithm for computing $p(c_{ti} \mid e_1, \dots, e_T)$ for any time step $t$ and car $i$. Your algorithm should not be exponential in $K$ or $T$.
   A description of the factor graph/Bayesian net used to model the problem, including any relevant variables and conditional probabilities. Also, a description of how you would use the factor graph to compute the provided probability. Note that you should try to simplify your expression for the probability as much as possible given the information provided.