In this homework, we consider two tasks: word segmentation and vowel insertion. Word segmentation often comes up when processing many non-English languages, in which words might not be flanked by spaces on either end, such as written Chinese or long compound German words.^[1] Vowel insertion is relevant for languages like Arabic or Hebrew, where modern script eschews notations for vowel sounds and the human reader infers them from context.^[2] More generally, this is an instance of a reconstruction problem with a lossy encoding and some context.

We already know how to optimally solve any particular search problem with graph search algorithms such as uniform cost search or A*. Our goal here is modeling — that is, converting real-world tasks into state-space search problems.

Our algorithm will base its segmentation and insertion decisions on the cost of processed text according to a language model. A language model is some function of the processed text that captures its fluency.

A very common language model in NLP is an $n$-gram sequence model. This is a function that, given $n$ consecutive words, provides a cost based on the negative log likelihood that the $n$-th word appears just after the first $n-1$ words.^[3] The cost will always be positive, and lower costs indicate better fluency.^[4] As a simple example: In a case where $n=2$ and $c$ is our $n$-gram cost function, $c($big, fish$)$ would be low, but $c($fish, fish$)$ would be fairly high.

Furthermore, these costs are additive: For a unigram model $u$ ($n = 1$), the cost assigned to $[w_1, w_2, w_3, w_4]$ is \[ u(w_1) + u(w_2) + u(w_3) + u(w_4). \] Similarly, for a bigram model $b$ ($n = 2$), the cost is \[ b(w_0, w_1) + b(w_1, w_2) + b(w_2, w_3) + b(w_3, w_4), \] where $w_0$ is -BEGIN-, a special token that denotes the beginning of the sentence.

We have estimated $u$ and $b$ based on the statistics of $n$-grams in text. Note that any words not in the corpus are automatically assigned a high cost, so you do not have to worry about that part.

A note on low-level efficiency and expectations: This assignment was designed considering input sequences of length no greater than roughly 200, where these sequences can be sequences of characters or of list items, depending on the task. Of course, it's great if programs can tractably manage larger inputs, but it's okay if such inputs can lead to inefficiency due to overwhelming state space growth.

In word segmentation, you are given as input a string of alphabetical characters ([a-z]) without whitespace, and your goal is to insert spaces into this string such that the result is the most fluent according to the language model.

1. Consider the following greedy algorithm: Begin at the front of the string. Find the ending position for the next word that minimizes the language model cost. Repeat, beginning at the end of this chosen segment.

   Show that this greedy search is suboptimal. In particular, provide an example input string on which the greedy approach would fail to find the lowest-cost segmentation of the input.

   In creating this example, you are free to design the $n$-gram cost function — both the choice of $n$ and the cost of any $n$-gram sequences — but costs must be positive, and lower cost should indicate better fluency. Note that the cost function doesn't need to be explicitly defined. You can just point out the relative cost of different word sequences that are relevant to the example you provide. And your example should be based on a realistic English word sequence — don't simply use abstract symbols with designated costs. Limit your answers to 4 sentences max to receive full credits.

   A specific (realistic) example explained within a couple of sentences.

2. Implement an algorithm that, unlike the greedy algorithm, finds the optimal word segmentation of an input character sequence. Your algorithm will consider costs based simply on a unigram cost function. UniformCostSearch (UCS) is implemented for you in util.py, and you should make use of it here. ^[5]

   Before jumping into code, you should think about how to frame this problem as a state-space search problem. How would you represent a state? What are the successors of a state? What are the state transition costs? (You don't need to answer these questions in your writeup.)

   Fill in the member functions of the SegmentationProblem class and the segmentWords function. The argument unigramCost is a function that takes in a single string representing a word and outputs its unigram cost. You can assume that all of the inputs would be in lower case. The function segmentWords should return the segmented sentence with spaces as delimiters, i.e. ' '.join(words).

   For convenience, you can actually run python submission.py to enter a console in which you can type character sequences that will be segmented by your implementation of segmentWords. To request a segmentation, type seg mystring into the prompt. For example:

         >> seg thisisnotmybeautifulhouse
   
           Query (seg): thisisnotmybeautifulhouse
   
           this is not my beautiful house
       

   Console commands other than seg — namely ins and both — will be used in the upcoming parts of the assignment. Other commands that might help with debugging can be found by typing help at the prompt.

   Hint: You are encouraged to refer to NumberLineSearchProblem and GridSearchProblem implemented in util.py for reference. They don't contribute to testing your submitted code but only serve as a guideline for what your code should look like.

   Hint: The actions that are valid for the ucs object can be accessed through ucs.actions.

   An implementation of the member functions of the SegmentationProblem class and the segmentWords function.

Now you are given a sequence of English words with their vowels missing (A, E, I, O, and U; never Y). Your task is to place vowels back into these words in a way that maximizes sentence fluency (i.e., that minimizes sentence cost). For this task, you will use a bigram cost function.

You are also given a mapping possibleFills that maps any vowel-free word to a set of possible reconstructions (complete words).^[6] For example, possibleFills('fg') returns set(['fugue', 'fog']).

1. Consider the following greedy-algorithm: from left to right, repeatedly pick the immediate-best vowel insertion for the current vowel-free word, given the insertion that was chosen for the previous vowel-free word. This algorithm does not take into account future insertions beyond the current word.

   Show, as in problem 1, that this greedy algorithm is suboptimal, by providing a realistic counter-example using English text. Make any assumptions you'd like about possibleFills and the bigram cost function, but bigram costs must remain positive. Limit your answers to 4 sentences max to receive full credits.

   A specific (realistic) example explained within a couple of sentences.

2. Implement an algorithm that finds optimal vowel insertions. Use the UCS subroutines.

   When you've completed your implementation, the function insertVowels should return the reconstructed word sequence as a string with space delimiters, i.e. ' '.join(filledWords). Assume that you have a list of strings as the input, i.e. the sentence has already been split into words for you. Note that the empty string is a valid element of the list.

   The argument queryWords is the input sequence of vowel-free words. Note that the empty string is a valid such word. The argument bigramCost is a function that takes two strings representing two sequential words and provides their bigram score. The special out-of-vocabulary beginning-of-sentence word -BEGIN- is given by wordsegUtil.SENTENCE_BEGIN. The argument possibleFills is a function that takes a word as a string and returns a set of reconstructions.

   Since we use a limited corpus, some seemingly obvious strings may have no filling, such as chclt -> {}, where chocolate is actually a valid filling. Don't worry about these cases.

   Note: If some vowel-free word $w$ has no reconstructions according to possibleFills, your implementation should consider $w$ itself as the sole possible reconstruction. Otherwise you should always use one of its possible completions according to possibleFills.

   Use the ins command in the program console to try your implementation. For example:

         >> ins thts m n th crnr
   
           Query (ins): thts m n th crnr
   
           thats me in the corner
       

   The console strips away any vowels you do insert, so you can actually type in plain English and the vowel-free query will be issued to your program. This also means that you can use a single vowel letter as a means to place an empty string in the sequence. For example:

         >> ins its a beautiful day in the neighborhood
   
           Query (ins): ts  btfl dy n th nghbrhd
   
           its a beautiful day in the neighborhood
       

   An implementation of the member functions of the VowelInsertionProblem class and the insertVowels function.

We'll now see that it's possible to solve both of these tasks at once. This time, you are given a whitespace-free and vowel-free string of alphabetical characters. Your goal is to insert spaces and vowels into this string such that the result is as fluent as possible. As in the previous task, costs are based on a bigram cost function.

1. Consider a search problem for finding the optimal space and vowel insertions. Formalize the problem as a search problem: What are the states, actions, costs, initial state, and end test? Try to find a minimal representation of the states.

   A formal definition of the search problem with definitions for the states, actions, costs, initial state, and end test.

2. Implement an algorithm that finds the optimal space and vowel insertions. Use the UCS subroutines.

   When you've completed your implementation, the function segmentAndInsert should return a segmented and reconstructed word sequence as a string with space delimiters, i.e. ' '.join(filledWords).

   The argument query is the input string of space- and vowel-free words. The argument bigramCost is a function that takes two strings representing two sequential words and provides their bigram score. The special out-of-vocabulary beginning-of-sentence word -BEGIN- is given by wordsegUtil.SENTENCE_BEGIN. The argument possibleFills is a function that takes a word as a string and returns a set of reconstructions.

   Note: In problem 2, a vowel-free word could, under certain circumstances, be considered a valid reconstruction of itself. However, for this problem, in your output, you should only include words that are the reconstruction of some vowel-free word according to possibleFills. Additionally, you should not include words containing only vowels such as a or i or out of vocabulary words; all words should include at least one consonant from the input string and a solution is guaranteed. Additionally, aim to use a minimal state representation for full credit.

   Use the command both in the program console to try your implementation. For example:

         >> both mgnllthppl
   
           Query (both): mgnllthppl
   
           imagine all the people
       

   An implementation of the member functions of the JointSegmentationInsertionProblem class and the segmentAndInsert function.

We'll now see a basic application of A* search in the context of everyone's favorite robot, Karel! In our context, Karel has a cookie craving and is trying to reach the cell with the cookie in the fewest number of moves while not entering the lava lake. Karel is hungry and aims to use A* search to optimize the cookie search and needs your help. Note that Karel can only use the following commands: turnLeft(), turnRight(), moveForward().

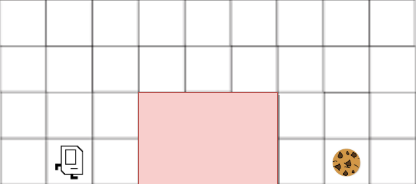
1. Assume the bottom left cell in the grid shown above is $(0, 0)$ in the Cartesian plane and then define $C^{*}(a, b)$ to be the minimum number of moves Karel needs to reach the cookie from cell $(a, b)$. Assume that Karel now has an admissable heuristic $h(a, b)$. What can we say about how $h(1, 0)$ compares to $C^{*}(1, 0)$?

   A mathematical expression relating $h(1, 0)$ to $C^{*}(1, 0)$ along with a justification.

2. How would we define an admissable heuristic $h(a, b)$ for Karel as described in part a)? In particular, how could we relax Karel's search problem to define a different cost metric that is always optimistic? Note that the final (cell) position of the cookie is always known by Karel.

   A description of a relaxed search problem and a definition of a different cost metric with a justification for why it is always optimistic.

[1] In German, Windschutzscheibenwischer is "windshield wiper". Broken into parts: wind ~ wind; schutz ~ block / protection; scheiben ~ panes; wischer ~ wiper.

[2] See https://en.wikipedia.org/wiki/Abjad.

[3] This model works under the assumption that text roughly satisfies the Markov property.

[4] Modulo edge cases, the $n$-gram model score in this assignment is given by $\ell(w_1, \ldots, w_n) = -\log(p(w_n \mid w_1, \ldots, w_{n-1}))$. Here, $p(\cdot)$ is an estimate of the conditional probability distribution over words given the sequence of previous $n-1$ words. This estimate is gathered from frequency counts taken by reading Leo Tolstoy's War and Peace and William Shakespeare's Romeo and Juliet.

[5] Solutions that use UCS ought to exhibit fairly fast execution time for this problem, so using A* here is unnecessary.

[6] This mapping was also obtained by reading Tolstoy and Shakespeare and removing vowels.