
We've created a LaTeX template here for you to use that contains the prompts for each question.

What courses should you take in a given quarter? Answering this question requires balancing your interests, satisfying prerequisite chains, graduation requirements, availability of courses; this can be a complex tedious process. In this assignment, you will write a program that does automatic course scheduling for you based on your preferences and constraints. The program will cast the course scheduling problem (CSP) as a constraint satisfaction problem (CSP) and then use backtracking search to solve that CSP to give you your optimal course schedule.
You will first get yourself familiar with the basics of CSPs in Problem 0. In Problem 1, you will implement a heuristic you learned from lecture that will make CSP solving much faster. Lastly, in Problem 2, you will create the course scheduling CSP and solve it using the code from previous parts.
Your goal is to turn on all the light bulbs by pressing a subset of the buttons.
Construct a CSP to solve this problem.
Your CSP should have $m$ variables and $n$ constraints.
For this problem only, you can use $m$-ary constraints:
constraints that can be functions of up to $m$ variables.
Describe your CSP precisely and concisely.
You need to specify the variables with their domain,
and the constraints with their scope and expression.
Make sure to include $T_j$ in your answer.
Hint: If stuck, take a look at parts (b) and (c) of this problem to see how
you could define the constraints using a boolean operator.
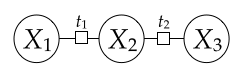
Backtrack() algorithm as defined in the lectures is a recursive algorithm,
where new instances of Backtrack() are called within parent instances of
Backtrack().
In this problem, we will ask you to produce the call stack for a specific call to Backtrack().
A call stack is just a diagram tracing out every recursive call. For our purposes,
for each call to Backtrack() you should specify which variable is being assigned,
the current domains, and which parent call to Backtrack() it's called within. For example,
if the order in which we assign variables is $X_1$, $X_2$, $X_3$, the call stack would be as follows:
| {[01], [01], [01]} | $\xrightarrow{X_1=0}$ | {0, [01], [01]} | $\xrightarrow{X_2=1}$ | {0, 1, [01]} | $\xrightarrow{X_3=0}$ | {0, 1, 0} |
| $\xrightarrow{X_1=1}$ | {1, [01], [01]} | $\xrightarrow{X_2=0}$ | {1, 0, [01]} | $\xrightarrow{X_3=1}$ | {1, 0, 1} |
The notation
Backtrack() is not called
when there's an inconsistent partial assignment ($\delta=0$); for example, we don't call
Backtrack() on $X_2 = 1$ when $X_1$ is already set to 1.
Using this call stack, we can produce the list of calls in the order they are explored. For this example where we assign variables in order $X_1$, $X_2$, $X_3$, the list would be $\{[01], [01], [01]\}, \{0, [01], [01]\}, \{0, 1, [01]\}, \{0, 1, 0\}, \{1, [01], [01]\}, \{1, 0, [01]\}, \{1, 0, 1\}$.
Suppose we assign variables in the order $X_3$, $X_1$, $X_2$.
Write the list of calls in the order they are explored and draw out the call-stack.
How many calls do we make to Backtrack()? Why can this number change depending on the ordering?
Backtrack() from your call stack in the previous question would we skip
if we use AC-3? Briefly explain why we skip (or don't skip) calls in this search with AC-3.
Backtrack() is called,
and an explanation for why this number can change based on the order in which you assign
variables (1-4 sentences).
For this problem only you may hand-draw a call stack and paste a picture into the
PDF, provided that the drawing is neat and everything is legible.
For iii., the number of calls to Backtrack() that get skipped along with an
explanation for why we skip these calls with AC-3 (1-2 sentences).
create_chain_csp() by
creating a generic chain CSP with XOR as factors.
Note: We've provided you with a CSP implementation
in util.py which supports unary and binary factors. For
now, you don't need to understand the implementation, but please read the
comments and get yourself familiar with the CSP interface. For this
problem, you'll need to use CSP.add_variable() and
CSP.add_binary_factor().
We'll now pivot towards creating more complicated CSPs, and solving them faster using heuristics.
Notice we are already able to solve the CSPs because in submission.py,
a basic backtracking search is already implemented. For this problem,
we will work with unweighted CSPs that can only have True/False factors;
a factor outputs 1 if a constraint is satisfied and 0 otherwise.
The backtracking search operates over partial assignments, and specifies whether
or not the current assignment satisfies all relevant constraints.
When we assign a value to a new variable $X_i$, we check that all constraints
that depend only on $X_i$ and the previously assigned variables are satisfied.
The function satisfies_constraints() returns whether or not
these new factors are satisfied based on the unaryFactors
and binaryFactors.
When satisfies_constraints() returns False, any full assignment that extends
the new partial assignment cannot satisfy all of the constraints,
so there is no need to search further with that new partial assignment.
Take a look at BacktrackingSearch.reset_results() to see the other fields
which are set as a result of solving the weighted CSP.
You should read submission.BacktrackingSearch carefully to make
sure that you understand how the backtracking search is working on the CSP.
create_nqueens_csp() by
adding $n$ variables and some number of binary factors.
Note that the solver collects some basic
statistics on the performance of the algorithm. You should take advantage of
these statistics for debugging and analysis.
You should get 92 (optimal) assignments for
$n=8$ with exactly 2057 operations (number of calls to backtrack()).
Hint: If you get a larger number of operations or your code times out on the test cases, make sure your CSP is minimal. Try to define the variables such that the size of domain is O(n).
Note: Please implement the domain of variables as 'list' type in Python.
You can refer to create_map_coloring_csp() and create_weighted_csp()
in util.py as examples of CSP problem implementations.
You can try these examples out by running:
python run_p1.py
satisfies_constraints() on
$X_j=a$ returns True).
Implement this heuristic in get_unassigned_variable() under the condition
self.mcv = True. It should take you exactly 1361 operations to find all
optimal assignments for 8 queens CSP — that's 30% fewer!
Some useful fields:
BacktrackingSearch, if var has been assigned a value,
you can retrieve it using assignment[var]. Otherwise var is not in
assignment.
In this problem, you will leverage our CSP solver for the problem of course scheduling.
We have scraped a subset of courses that are offered from Stanford's
Bulletin. For each course in this dataset,
we have information on which quarters it is offered,
the prerequisites (which may not be fully accurate due to
ambiguity in the listing), and the range of units allowed.
You can take a look at all the courses in courses.json.
Please refer to
util.Course and util.CourseBulletin for more information.
To specify a desired course plan, you would need to provide a profile
which specifies your constraints and preferences for courses.
A profile is specified in a text file (see profile*.txt for examples).
The profile file has four sections:
minUnits 0
maxUnits 3
register for the quarters that you want
to take your courses in. For example,
register Aut2019would sign you up for this academic year. The quarters need not be contiguous, but they must follow the exact format
register Win2020
register Spr2020
XxxYYYY where Xxx is one of Aut, Win, Spr, Sum
and YYYY is the year.
taken keyword.
For example, if you're in CS221, this is probably what you would put:
taken CS103
taken CS106B
taken CS107
taken CS109
request.
For example, two basic requests would look like this:
request CS224NNot every request must be fulfilled, and indeed, due to the additional constraints described below, it is possible that not all of them can actually be fulfilled.
request CS229
Constrained requests. To allow for more flexibility in your preferences, we allow some freedom to customize the requests:
request CS229 or CS229A or CS229TNote that these courses do not necessarily have to be offered in the same quarter. The final schedule can have at most one of these three courses. Each course can only be requested at most once.
in modifier.
For example, if you want to take one of CS221 or CS229 in either Aut2018 or Sum2019, do:
request CS221 or CS229 in Aut2018,Sum2019If you do not specify any quarters, then the course can be taken in any quarter.
after, which specifies
that a course must be taken after another one.
For example, if you want to choose one of CS221 or CS229 and take it after
both CS109 and CS161, add:
request CS221 or CS229 after CS109,CS161Note that this implies that if you take CS221 or CS229, then you must take both CS109 and CS161. In this case, we say that CS109 and CS161 are
prereqs of this request.
(Note that there's no space after the comma.)
If you request
course A and B (separately), and A is an official prerequisite of B based on
the CourseBulletin,
we will automatically add A as a prerequisite for B; that is,
typing request B is equivalent to request B after A.
Additionally, if A is a prerequisite of B, in order to request B
you must either request A or declare you've taken A before.
weight, which adds
non-negative weight to each request.
To accommodate this, we will work with a standard CSP (as opposed to unweighted, like
Problem 1), which associates a weight for
each assignment $x$ based on the product of $m$ factor functions $f_1, \dots, f_m$:
$$\text{Weight}(x) = \prod^m_{j=1}f_j(x)$$
where each factor $f_j(x)\geq 0$.
Our goal is to find the assignment(s) $x$ with the highest weight.
Notice that our backtracking search already works with normal CSPs; you should
simply define factors that output real numbers.
For CSP construction, you can refer to the CSP examples we have provided
in util.py for guidance (create_map_coloring_csp() and
create_weighted_csp()).
All requests have a default weight value of 1. Requests with higher weight should be preferred by your CSP solver. Note that you can combine all of the aforementioned operators into one as follows (again, no space after comma):
request CS221 or CS229 in Win2018,Win2019 after CS131 weight 5
Each request line in your profile is represented in code
as an instance of the Request class (see util.py).
For example, the request above would have the following fields:
cids (course IDs that you're choosing one of) with value ['CS221', 'CS229']quarters (that you're allowed to take the courses) with value ['Win2018', 'Win2019']prereqs (course IDs that you must take before) with value ['CS131']weight (preference) with value 5.0
It's important to note that a request does not have to be fulfilled, but if it is,
the constraints specified by the various operators after,in must
also be satisfied.
You shall not worry about parsing the profiles because
we have done all the parsing of the bulletin and profile for you,
so all you need to work with is the collection of Request
objects in Profile and CourseBulletin
to know when courses are offered and the number of units of courses.
import util
# load bulletin
bulletin = util.CourseBulletin('courses.json')
# retrieve information of CS221
cs221 = bulletin.courses['CS221']
print(cs221)
# look at various properties of the course
print(cs221.cid)
print(cs221.minUnits)
print(cs221.maxUnits)
print(cs221.prereqs) # the prerequisites
print(cs221.is_offered_in('Aut2018'))
print(cs221.is_offered_in('Win2019'))
# load profile from profile_example.txt
profile = util.Profile(bulletin, 'profile_example.txt')
# see what it's about
profile.print_info()
# iterate over the requests and print out the properties
for request in profile.requests:
print(request.cids, request.quarters, request.prereqs, request.weight)
Solving the CSP.
Your task is to take a profile and bulletin and construct a CSP.
We have started you off with code in SchedulingCSPConstructor
that constructs the core variables of the CSP as well as some basic constraints.
The variables are all pairs of requests and registered quarters (request, quarter),
and the value of such a variable is one of the course IDs in that Request
or None, which indicates none of the courses should be taken in that
quarter. We will add auxiliary variables later.
We have also implemented some basic constraints:
add_bulletin_constraints(), which enforces that a course can only be
taken if it's offered in that quarter (according to the bulletin), and
add_norepeating_constraints(),
which constrains that no course can be taken more than once.
You should take a look at add_bulletin_constraints() and
add_norepeating_constraints() to get a basic understanding
how the CSP for scheduling is represented. Nevertheless, we'll highlight
some important details to make it easier for you to implement:
(request, quarter)
where request is a Request object
(like the one shown above)
and quarter is a str representing a quarter
(e.g. 'Aut2018'). For detail please look at
SchedulingCSPConstructor.add_variables().
quarter is all possible quarters
(self.profile.quarters, e.g. ['Win2016', 'Win2017']).
cid, you can get the corresponding
Course object by self.bulletin.courses[cid].
add_quarter_constraints() in submission.py.
This is when your profile specifies which quarter(s) you want your requested courses to be taken in.
This is not saying that one of the courses must be taken,
but if it is, then it must be taken in any one of the specified quarters.
Also note that this constraint will apply to all courses in that request.
add_unit_constraints().
(courseId, quarter)
to the CSP taking on a value equal to the number of units being taken for that
course during that quarter. When the course is not taken during that quarter,
the unit should be 0.
(request, quarter)
and (courseId, quarter) variables.
create_sum_variable() function we've implemented for you;
pay careful attention to the arguments.
Hint: If your code times out, your maxSum passed
to create_sum_variable() might be too large.
run_p2.py. Here is an example with
profile2b.txt as input:
python run_p2.py profile2b.txtRunning this command will print information that may be helpful for debugging, such as profile information, the number of optimal assignments found (along with their weight and the number of times
backtrack() is called while solving the CSP), one full optimal assignment,
and the resulting course schedule.
profile.txt (take a look at some of the profile text files
included in the assignment's main directory for inspiration) and then run the course scheduler:
python run_p2.py profile.txtIf the courses you wish to schedule are not listed in
courses.json,
feel free to add them in as you please! In addition, feel free to modify course
details as well (e.g., you can change the list of quarters that a course is
being offered in if it does not match the information on the current year's course calendar).
You might want to turn on the appropriate heuristic flags to speed up the
computation; in particular, self.ac3 = True applies the arc-consistency heuristic
that we implement for you, and you can use your own MCV implementation.
Does it produce a reasonable course schedule?
Please include your profile.txt and the best schedule in your writeup
(you can just paste it into the pdf that you submit);
we're curious how it worked out for you! Please include your schedule and the profile in the PDF;
otherwise you will not receive credit.
courses.json
(if applicable; for example, if you added courses).
Medical residents are often scheduled to work long shifts with insufficient rest, leading to exhaustion and burnout. This can negatively affect the residents and potentially lead to mistakes that also negatively affect the patients in their care [1]. A hospital could use a constraint-satisfaction approach to try to create a work schedule that respects the “on-call night, day-off, rest period, and total work-hour regulations mandated by the Accreditation Council for Graduate Medical Education, as well as the number of residents needed each hour given the demand (aka number of patients and procedures scheduled) [2]. The constraints are:
Let’s assume for a given hospital that the constraints listed above were collectively unsatisfiable given the number of residents assigned to that hospital. However, its formulation as an unsatisfiable CSP depends on other factors remaining fixed, such as