Pac-Man, now with ghosts.
Minimax, Expectimax.

Introduction

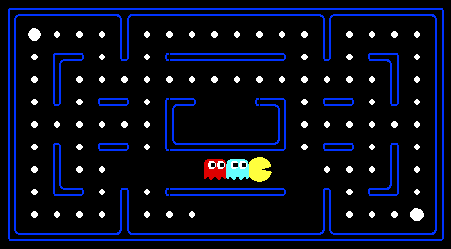
For those of you not familiar with Pac-Man, it's a game where Pac-Man (the yellow circle with a mouth in the above figure) moves around in a maze and tries to eat as many food pellets (the small white dots) as possible, while avoiding the ghosts (the other two agents with eyes in the above figure). If Pac-Man eats all the food in a maze, it wins. The big white dots at the top-left and bottom-right corner are capsules, which give Pac-Man power to eat ghosts in a limited time window, but you won't be worrying about them for the required part of the assignment. You can get familiar with the setting by playing a few games of classic Pac-Man, which we come to just after this introduction.

In this assignment, you will design agents for the classic version of Pac-Man, including ghosts. Along the way, you will implement both minimax and expectimax search.

The base code for this assignment contains a lot of files, which are listed towards the end of this page; you, however, do not need to go through these files to complete the assignment. These are present only to guide the more adventurous amongst you to the heart of Pac-Man. As in previous assignments, you will only be modifying submission.py.

  python --version
  

conda create --name cs221 python=3.12

conda activate cs221

We've created a LaTeX template here for you to use that contains the prompts for each question.

Important Note: Please Read

Warmup

First, play a game of classic Pac-Man to get a feel for the assignment:

python pacman.py

Now, run the provided ReflexAgent in submission.py:

python pacman.py -p ReflexAgent

python pacman.py -p ReflexAgent -l testClassic

python pacman.py -p ReflexAgent -k 1

python pacman.py -p ReflexAgent -k 2

Note: You can never have more ghosts than the layout permits.

Options: Default ghosts are random; you can also play for fun with slightly smarter directional ghosts using -g DirectionalGhost. You can also play multiple games in a row with -n and an integer indicating the number of games to play. Turn off graphics with -q to run lots of games quickly.

Now that you are familiar enough with the interface, inspect the ReflexAgent code carefully (in submission.py) and make sure you understand what it's doing. The reflex agent code provides some helpful examples of methods that query the GameState: A GameState object specifies the full game state, including the food, capsules, agent configurations, and score changes: see submission.py for further information and helper methods, which you will be using in the actual coding part. We are giving an exhaustive and very detailed description below, for the sake of completeness and to save you from digging deeper into the starter code. The actual coding part is very small -- so please be patient if you think there is too much writing.

Note: If you wish to run the game in the terminal using a text-based interface, check out the terminal directory.

Note 2: If the action tiebreaking is done deterministically for Problems 1, 2, and 3, running on the mediumClassic map may cause mostly losses. This is alright since the grader test cases don’t run on these layouts.

Problem 1: Minimax

1. Before you code up Pac-Man as a minimax agent, notice that instead of just one ghost, Pac-Man could have multiple ghosts as adversaries. We will extend the minimax algorithm from class, which had only one min stage for a single adversary, to the more general case of multiple adversaries. In particular, your minimax tree will have multiple min layers (one for each ghost) for every max layer.
   

   Formally, consider the limited depth tree minimax search with evaluation functions taught in class. Suppose there are $n+1$ agents on the board, $a_0,\ldots , a_n$, where $a_0$ is Pac-Man and the rest are ghosts. Pac-Man acts as a max agent, and the ghosts act as min agents. A single depth consists of all $n+1$ agents making a move, so depth 2 search will involve Pac-Man and each ghost moving two times. In other words, a depth of 2 corresponds to a height of $2(n+1)$ in the minimax game tree (see diagram below).

   

   Comment: In reality, all the agents move simultaneously. In our formulation, actions at the same depth happen at the same time in the real game. To simplify things, we process Pac-Man and ghosts sequentially. You should just make sure you process all of the ghosts before decrementing the depth.

   Before diving into the recurrence, let's understand our notation. In the recurrence for $V_{\text{minmax}}(s,d)$, $s$ represents the current state, and $d$ represents the current depth in the game tree, with $d = d_{\text{max}}$ indicating the root of the tree (initial state) and decreasing as we go deeper into the tree.

   Write the recurrence for $V_{\text{minmax}}(s,d)$ in math as a piecewise function. You should express your answer in terms of the following functions:

   • $\text{IsEnd}(s)$, which tells you if $s$ is an end state.
   • $\text{Utility}(s)$, the utility of a state $s$.
   • $\text{Eval}(s)$, an evaluation function for the state $s$.
   • $\text{Player}(s)$, which returns the player whose turn it is in state $s$. Ensure you specify conditions like $\textrm{if}~ \text{Player}(s) = a_0$ clearly.
   • $\text{Actions}(s)$, which returns the possible actions that can be taken from state $s$.
   • $\text{Succ}(s,a)$, which returns the successor state resulting from taking an action $a$ at a certain state $s$.

   You may use $n$ anywhere in your solution without explicitly passing it in as an argument. You should not have $d_{\text{max}}$ in your solution. Please stick to notations and terms as described here, and avoid introducing personal variations without clear definitions. Remember, clarity is essential. You may use any relevant notation introduced in lecture.

   Hint: It will be helpful to review the lecture slides about "Depth-limited search".

2. Now fill out the MinimaxAgent class in submission.py using the above recurrence. Remember that your minimax agent (Pac-Man) should work with any number of ghosts, and your minimax tree should have multiple min layers (one for each ghost) for every max layer.

   Your code should be able to expand the game tree to any given depth. Score the leaves of your minimax tree with the supplied self.evaluationFunction, which defaults to scoreEvaluationFunction. The class MinimaxAgent extends MultiAgentSearchAgent, which gives access to self.depth and self.evaluationFunction. Make sure your minimax code makes reference to these two variables where appropriate, as these variables are populated from the command line options.

   Implementation Hints

   • Read the comments in submission.py thoroughly before starting to code!
   • Pac-Man is always agent 0, and the agents move in order of increasing agent index. Use self.index in your minimax implementation to refer to the Pac-Man's index. Notice that only Pac-Man will actually be running your MinimaxAgent.
   • All states in minimax should be GameStates, either passed in to getAction or generated via GameState.generateSuccessor. In this assignment, you will not be abstracting to simplified states.
   • You might find the functions described in the comments to the ReflexAgent and MinimaxAgent useful.
   • $\text{Utility}(s)$ should be the final game score, returned from GameState.getScore.
   • The evaluation function for this part is already written (self.evaluationFunction), and you should call this function without changing it. Use self.evaluationFunction in your definition of $V_\text{minmax}$ wherever you used $\text{Eval}(s)$ in part $1a$. Recognize that now we're evaluating states rather than actions. Look-ahead agents evaluate future states whereas reflex agents evaluate actions from the current state.
   • If there is a tie between multiple actions for the best move, you may break the tie however you see fit.
   • The minimax values $V_\text{minmax}$ of the initial state in the minimaxClassic layout are 9, 8, 7, and -492 for depths 1, 2, 3, and 4, respectively (passed into the “-a depth=[depth]” argument). You can use these numbers to verify whether your implementation is correct. To verify, you can print your calculated minimax value in getAction and check if the value of the initial state (first value that appears) is equal to the value listed above. Note that your Pac-Man agent will often win, despite the dire prediction of depth 4 minimax search, whose command is shown below. With depth 4, our Pac-Man agent wins 50-70% of the time. Depths 2 and 3 will give a lower win rate. Be sure to test on a large number of games using the -n and -q flags. Check the instructions in "Warmup" for more details on running multiple games in a row.

     python pacman.py -p MinimaxAgent -l minimaxClassic -a depth=4

   • One "depth" includes Pac-Man and all of the ghost agents.
   Further Observations

   These questions and observations are here for you to ponder upon; no need to include in the write-up.

   • On larger boards such as openClassic and mediumClassic (the default), you'll find Pac-Man to be good at not dying, but quite bad at winning. It will often thrash around without making progress. It might even thrash around right next to a dot without eating it. Don't worry if you see this behavior. Why does Pac-Man thrash around right next to a dot?
     
     
     Click to see our thoughts!

     Part of the reason this happens is because there could be ties between different possible sequences of actions but no intelligent tie-breaking, as well as not having 'memory' of deciding to follow a sequence of actions. There could be other factors that also play into this as well.

Problem 2: Alpha-beta pruning

1. Make a new agent that uses alpha-beta pruning to more efficiently explore the minimax tree in AlphaBetaAgent. Again, your algorithm will be slightly more general than the pseudo-code in the slides, so part of the challenge is to extend the alpha-beta pruning logic appropriately to multiple ghost agents.

   You should see a speed-up: Perhaps depth 3 alpha-beta will run as fast as depth 2 minimax. Ideally, depth 3 on mediumClassic should run in just a few seconds per move or faster. To ensure your implementation does not time out, please observe the 0-point test results of your submission on Gradescope.

   python pacman.py -p AlphaBetaAgent -a depth=3

   The AlphaBetaAgent minimax values should be identical to the MinimaxAgent minimax values, although the actions it selects can vary because of different tie-breaking behavior. Again, the minimax values of the initial state in the minimaxClassic layout are 9, 8, 7, and -492 for depths 1, 2, 3, and 4, respectively. Running the command given above this paragraph, which uses the default mediumClassic layout, the minimax values of the initial state should be 9, 18, 27, and 36 for depths 1, 2, 3, and 4, respectively. Again, you can verify by printing the computed minimax value of the initial state passed into getAction. Note when comparing the time performance of the AlphaBetaAgent to the MinimaxAgent, make sure to use the same layouts for both. You can manually set the layout by adding for example -l minimaxClassic to the command given above this paragraph.

Problem 3: Expectimax

1. Random ghosts are of course not optimal minimax agents, so modeling them with minimax search is not optimal. Instead, write down the recurrence for $V_{\text{exptmax}}(s,d)$, which is the maximum expected utility against ghosts that each follow the random policy, which chooses a legal move uniformly at random.
   Your recurrence should resemble that of problem 1a, which means that you should write it in terms of the same functions that were specified in problem 1a.
2. Fill in ExpectimaxAgent, where your Pac-Man agent no longer assumes ghost agents take actions that minimize Pac-Man's utility. Instead, Pac-Man tries to maximize its expected utility and assumes it is playing against multiple RandomGhosts, each of which chooses from getLegalActions uniformly at random.

   You should now observe a more cavalier approach to close quarters with ghosts. In particular, if Pac-Man perceives that it could be trapped but might escape to grab a few more pieces of food, it will at least try.

   python pacman.py -p ExpectimaxAgent -l trappedClassic -a depth=3

   You may have to run this scenario a few times to see Pac-Man's gamble pay off. Pac-Man would win half the time on average, and for this particular command, the final score would be -502 if Pac-Man loses and 532 or 531 (depending on your tiebreaking method and the particular trial) if it wins. You can use these numbers to validate your implementation.

   Why does Pac-Man's behavior as an expectimax agent differ from its behavior as a minimax agent (i.e., why doesn't it head directly for the ghosts)? We'll ask you for your thoughts in Problem 5.

Problem 4: Evaluation function (extra credit)

• If you would like to participate in the extra credit, please submit the same submission.py to both the HW5 Programming and HW5 Programming (extra credit) assignments on Gradescope.
• On Gradescope, your programming assignment will be graded out of 30 points total (including basic and hidden tests). However, there is an opportunity to earn up to 12 extra credit points (10 programming and 2 written), as described below.
• CAs will not be answering specific questions about extra credit; this part is on your own!

1. Write a better evaluation function for Pac-Man in the provided function betterEvaluationFunction. The evaluation function should evaluate states rather than actions. You may use any tools at your disposal for evaluation, including any util.py code from the previous assignments. With depth 2 search, your evaluation function should clear the smallClassic layout with two random ghosts more than half the time for full (extra) credit and still run at a reasonable rate.

   python pacman.py -l smallClassic -p ExpectimaxAgent -a evalFn=better -q -n 20

   For this question, we will run your Pac-Man agent 20 times with a time limit of 10 seconds and your implementations of questions 1-3. We will calculate the average score you obtained in the winning games if you win more than half of the 20 games. You obtain 1 extra point per 100 point increase above 1200 in your average winning score, for a maximum of 5 points. In grader.py, you can see how extra credit is awarded. For example, you get 2 points if your average winning score is between 1400 and 1500. In addition, the top 3 people in the class will get additional points of extra credit: 5 for the winner, 3 for the runner-up, and 1 for third place. Note that late days can only be used for non-leaderboard extra credit. If you want to get extra credit from the leaderboard, please submit before the normal deadline.
   
   You will be added to the leaderboard automatically when you submit. You can access the leaderboard by opening your submission on Gradescope and clicking "Leaderboard" on the top right corner.

   Hints and Observations

   • Having gone through the rest of the assignment, you should play Pac-Man again yourself and think about what kinds of features you want to add to the evaluation function. How can you add multiple features to your evaluation function?
   • You may want to use the reciprocal of important values rather than the values themselves for your features.
   • The betterEvaluationFunction should run in the same time limit as the other problems.
2. Clearly describe your evaluation function. What is the high-level motivation? Also talk about what else you tried, what worked, and what didn't. Please write your thoughts in pacman.pdf, not in code comments. Note that you can attempt this question only if you have implemented a different evaluation function in part (a) above.
   A short paragraph answering the questions above.

Problem 5: AI (Mis)Alignment and Reward Hacking

Before diving into the problem, it would be beneficial to refer to the AI alignment module to gain deeper insights and context:

• Video
• PDF

In this problem we'll revisit the differences between our minimax and expectimax agents, and reflect upon the broader consequences of AI misalignment: when our agents don't do what we want them to do, or technically do, but cause unintended consequences along the way. Going back to Problem 3, consider the following runs of the minimax and expectimax agents on the small trappedClassic environment:

python pacman.py -p MinimaxAgent -l trappedClassic -a depth=3

python pacman.py -p ExpectimaxAgent -l trappedClassic -a depth=3

Be sure to run each command a few times, as there is some randomness in the environment and the agents' behaviors, and pay attention, as the episode lengths can be quite short. You can always add --frameTime 1 to the command line so the game pauses after every frame. What you should see is that the minimax agent will always rush towards the closest ghost, while the expectimax agent will occasionally be able to pick up all of the pellets and win the episode. (If you don't see this behavior, your implementations could be incorrect!) Then answer the following questions:

1. Describe why the behavior of the minimax and expectimax agents differ. In particular, why does the minimax agent, seemingly counterintuitively, always rush the closest ghost (instead of the further ghost), while the expectimax agent (occasionally) doesn't?
   One sentence why the minimax agent always rushes the closest ghost and not the further ghost, and one sentence why the expectimax agent doesn't. Specifically, please state the assumptions made by minimax because of which this phenomenon occurs.
   
   
2. We might say that the Minimax agent suffers from an alignment problem: the agent optimizes an objective that we have designed (our state evaluation function), but in some scenarios leads to suboptimal or unintended behavior (e.g. dying instantly). Often the burden is on the designer/programmer to design an objective that more accurately captures the behavior we want from the agent across scenarios. Suggest one potential change to the default state evaluation function $\text{Eval}(s)$ (i.e. scoreEvaluationFunction) and/or the default utility function $\text{Utility}(s)$ (i.e. the final game score) that would prevent the minimax agent from dying instantly in the trappedClassic environment, and behave more closely to that of the expectimax agent.
   1-2 sentences describing a change in the state evaluation/utility function(s) and why it would work. No need to code anything up, verify that the suggested change is actually accessible in the GameState object, or give concrete numbers; just describe the hypothetical change in the functions. An answer which suggests changes to how the game score is computed itself (which both $\text{Eval}(s)$ and $\text{Utility}(s)$ depend upon) will also be accepted.
3. Pacman's behavior above is an example of one concrete problem in AI alignment called reward hacking, which occurs when an agent satisfies some objective but may not actually fulfill the designer's intended goals, due e.g. to an imprecise definition of the objective function. As another example, a cleaning robot rewarded for minimizing the number of messes in a given space could optimize its reward function by hiding the messes under the rug. In this case, the agent finds a shortcut to optimize the reward, but the shortcut fails to attain the designer’s goals (see [1] for more examples).
   
   Even if the agent does satisfy the designer's goals, another problem can arise (again see this paper): the agent's behavior might cause negative side effects that come in conflict with broader values held by society or other stakeholders. For instance, a social media content recommendation system might aim to maximize user engagement, but in doing so, spread disinformation and conspiracy theories (since such posts get the most engagement), which is at odds with societal values.
   
   Can you think of another example of either of these problems?
   In 2-5 sentences describe another realistic scenario (outside Pacman) in which a designer might specify an objective, but the objective is either susceptible to reward hacking, or the resulting agent/model causes negative side effects. Please state if your example is an instance of reward hacking or negative side effects (or both) along with a brief justification to receive full credit.

Go Pac-Man Go!

[1] For more examples of reward hacking (or "specification gaming"), see this article from DeepMind and this list of concrete examples of reward hacking observed in the AI literature.